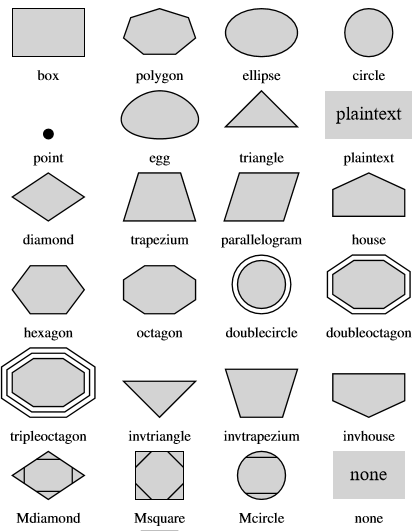
Les paramètres suivants permettent de personnaliser les cartes conceptuelles (couleurs, formes, etc.).
Ils sont facultatifs.
Blocs par défaut
Longueur maximale des citations
Couleur de fond du graphe
gris pâle
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de police
noir
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Type de police
Taille de police
Forme des blocs
Sans bordure
Boite
Polygone
Ellipse
Cercle
Point
Oeuf
Triangle
Losange
Trapèze
Parallèlogramme
Maison
Pentagone
Hexagone
Octogone
Double cercle
Double octogone
Triple octogone
Triangle inversé
Trapèze inversé
Maison inversée
Losange segmenté
Carré segmenté
Cercle segmenté
aucune
Couleur de fond des blocs
bleu acier
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de bordure des blocs
bleu acier
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Remplissage des blocs
Vide
Plein
Gras
Invisible
Taille des flèches
1
2
3
4
5
6
7
8
9
10
Couleur des flèches
rouge sombre
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
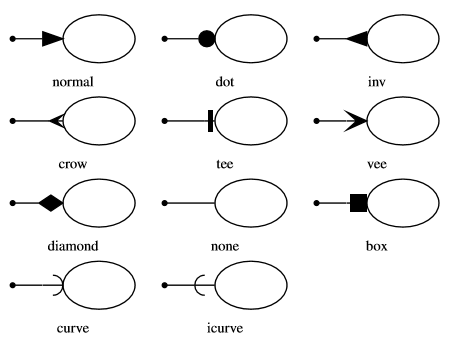
Tête des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Queue des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Sens des flèches
1 vers 2
2 vers 1
1 et 2
aucun sens
Bloc personnalisé
Nom de l'argument (bloc)
Couleur de police
noir
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Forme du bloc
Sans bordure
Boite
Polygone
Ellipse
Cercle
Point
Oeuf
Triangle
Losange
Trapèze
Parallèlogramme
Maison
Pentagone
Hexagone
Octogone
Double cercle
Double octogone
Triple octogone
Triangle inversé
Trapèze inversé
Maison inversée
Losange segmenté
Carré segmenté
Cercle segmenté
aucune
Couleur de fond du bloc
saumon
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de bordure du bloc
saumon
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Remplissage du bloc
Vide
Plein
Gras
Invisible
Bloc personnalisé
Nom de l'argument (bloc)
Couleur de police
noir
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Forme du bloc
Sans bordure
Boite
Polygone
Ellipse
Cercle
Point
Oeuf
Triangle
Losange
Trapèze
Parallèlogramme
Maison
Pentagone
Hexagone
Octogone
Double cercle
Double octogone
Triple octogone
Triangle inversé
Trapèze inversé
Maison inversée
Losange segmenté
Carré segmenté
Cercle segmenté
aucune
Couleur de fond du bloc
saumon
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de bordure du bloc
saumon
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Remplissage du bloc
Vide
Plein
Gras
Invisible
Bloc personnalisé
Nom de l'argument (bloc)
Couleur de police
noir
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Forme du bloc
Sans bordure
Boite
Polygone
Ellipse
Cercle
Point
Oeuf
Triangle
Losange
Trapèze
Parallèlogramme
Maison
Pentagone
Hexagone
Octogone
Double cercle
Double octogone
Triple octogone
Triangle inversé
Trapèze inversé
Maison inversée
Losange segmenté
Carré segmenté
Cercle segmenté
aucune
Couleur de fond du bloc
saumon
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de bordure du bloc
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Remplissage du bloc
Vide
Plein
Gras
Invisible
Flèche personnalisée
Nom du prédicat (flèche)
Couleur de police
noir
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de tracé des lignes
bleu acier
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Type de tracé des lignes
Plein
Gras
Pointillés
Invisible
Taille des flèches
1
2
3
4
5
6
7
8
9
10
Couleur des flèches
rouge sombre
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Tête des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Queue des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Sens des flèches
1 vers 2
2 vers 1
1 et 2
aucun sens
Flèche personnalisée
Nom du prédicat (flèche)
Couleur de police
noir
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de tracé des lignes
bleu acier
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Type de tracé des lignes
Plein
Gras
Pointillés
Invisible
Taille des flèches
1
2
3
4
5
6
7
8
9
10
Couleur des flèches
rouge sombre
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Tête des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Queue des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Sens des flèches
1 vers 2
2 vers 1
1 et 2
aucun sens
Flèche personnalisée
Nom du prédicat (flèche)
Couleur de police
noir
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de tracé des lignes
bleu acier
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Type de tracé des lignes
Plein
Gras
Pointillés
Invisible
Taille des flèches
1
2
3
4
5
6
7
8
9
10
Couleur des flèches
rouge sombre
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Tête des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Queue des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Sens des flèches
1 vers 2
2 vers 1
1 et 2
aucun sens
Flèche personnalisée
Nom du prédicat (flèche)
Couleur de police
noir
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Couleur de tracé des lignes
bleu acier
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Type de tracé des lignes
Plein
Gras
Pointillés
Invisible
Taille des flèches
1
2
3
4
5
6
7
8
9
10
Couleur des flèches
rouge sombre
black
dimgrey
grey
darkgrey
silver
lightgrey
gainsboro
whitesmoke
white
lavenderblush
palevioletred
crimson
pink
lightpink
maroon
darkred
red
firebrick
brown
indianred
lightcoral
rosybrown
snow
mistyrose
salmon
tomato
darksalmon
coral
orangered
lightsalmon
sienna
seashell
saddlebrown
chocolate
sandybrown
peachpuff
peru
linen
bisque
darkorange
burlywood
tan
antiquewhite
navajowhite
blanchedalmond
papayawhip
moccasin
orange
wheat
oldlace
floralwhite
darkgoldenrod
goldenrod
cornsilk
gold
khaki
lemonchiffon
palegoldenrod
darkkhaki
olive
yellow
lightgoldenrodyellow
lightyellow
beige
ivory
olivedrab
yellowgreen
darkolivegreen
greenyellow
chartreuse
lawngreen
darkgreen
green
lime
limegreen
forestgreen
lightgreen
palegreen
darkseagreen
honeydew
seagreen
mediumseagreen
springgreen
mintcream
mediumspringgreen
mediumaquamarine
aquamarine
turquoise
lightseagreen
mediumturquoise
teal
darkcyan
cyan
darkslategrey
paleturquoise
lightcyan
azure
darkturquoise
cadetblue
powderblue
lightblue
deepskyblue
skyblue
lightskyblue
steelblue
aliceblue
dodgerblue
slategrey
lightslategrey
lightsteelblue
cornflowerblue
royalblue
navy
darkblue
mediumblue
blue
midnightblue
lavender
ghostwhite
slateblue
mediumslateblue
darkslateblue
mediumpurple
blueviolet
indigo
darkorchid
darkviolet
mediumorchid
purple
darkmagenta
magenta
violet
plum
thistle
orchid
mediumvioletred
deeppink
hotpink
Tête des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Queue des flèches
normal
point
inversée
crow
té
vee
losange
aucune
carré
courbe
courbe inversée
cercle vide
point+inversée
cercle vide+inversée
vide
ouvert
Sens des flèches
1 vers 2
2 vers 1
1 et 2
aucun sens